4.9. シグモイド関数

\[h(x) = \frac{1} {1 + \exp(-x)}\]

\[h(x) = \frac{1} {1 + \exp(-ax)}\]

\(a\)をコントロールパラメータ(変更できる値)

import numpy as np
import matplotlib.pylab as plt

def sigmoid(x, a):
    """
    シグモイド関数

    Parameters
    ----------
    x: numpy.ndarray
        入力xの配列
    """
    return 1 / (1 + np.exp(-a * x))

def step_function(x):
    """
    入力xに対し、0 <= x の時は 0, x > 0 の時は1を返却する
    ステップ関数

    Parameters
    ----------
    x: numpy.ndarray
        入力xの配列
    """
    y = x > 0
    return y.astype(np.int)

x = np.arange(-5.0, 5.0, 0.1)
y1 = step_function(x)
y2 = sigmoid(x, 5)
y3 = sigmoid(x, 1)

plt.plot(x, y1, label="ステップ関数", ls="--")
plt.plot(x, y2, label="シグモイド関数")
plt.plot(x, y3, label="シグモイド関数")
plt.ylim(-0.1, 1.1)
plt.show()

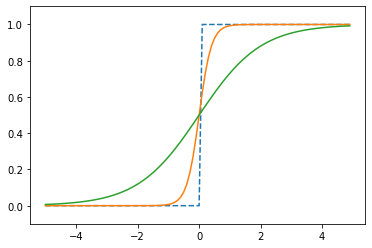
a の値を大きくしていくと、ステップ関数に近づく

4.10. なめらかとは

数学で、「連続した」という用語がある。値が連続していることを意味していて、数字が途切れたりしないことを言う。

「なめらか」というのは、連続した値であることと、微分が可能であるであることを言う。

ステップ関数、ReLU関数は微分できない。(ニューラルネットワークでは、ReLUを無理やり微分している)

• ReLUにもいろいろ